고체물리학의 핵심 - Dispersion relation의 의미 (2)

3. Crystal의 주기적 격자구조는 'some effective mass'를 발생시킨다 : 에너지(ħω) 보존, 운동량 ħk(quasi-momentum) = ħk1(crystal) + ħk2(wave)

결정에서 각주파수(ω)와 파동수(k) 사이의 분산 관계는 실제로 nontrivial일 수 있습니다. 분산 관계는 결정 격자의 주기적 포텐셜과 파동의 상호 작용에서 발생합니다. 상대론적 ħω-ħk 관계에서 사용되는 질량 개념은 결정에서 전파되는 파동의 경우에 직접 적용되지 않을 수 있다는 점에 유의하는 것이 중요합니다. 그러나 결정 격자가 효과적인 "질량" 또는 보다 정확하게는 파동의 거동을 변경하는 효과적인 상호 작용을 제공하는 결과로 nontrivial 분산 관계를 생각할 수 있습니다.

결정에서 파동과 격자 전위의 상호 작용은 밴드 구조라는 현상으로 이어지며, 여기서 파동의 에너지는 밴드 갭으로 분리된 불연속 에너지 밴드로 양자화됩니다. 이 거동은 에너지와 운동량이 연속적인 파동의 free space에서의 전파와는 상당히 다릅니다.

결정의 운동량 보존은 자유 공간에서보다 약간 더 미묘합니다. 파동이 결정과 상호 작용할 때 전체 운동량은 보존되지만 결정 자체의 운동량 보존에는 격자의 주기성에서 비롯된 추가 제한이 적용됩니다. 이러한 제한은 운동량과 유사한 양이지만 주기적 격자 구조를 고려한 quasi-momentum의 보존으로 나타납니다.

요약하면, 결정에서 nontrivial 분산 관계는 실제 질량을 갖는 결정으로 해석될 수 없지만, 파동의 거동을 수정하는 효과적인 상호 작용을 도입하는 결정 격자의 결과로 생각할 수 있습니다. 결정의 운동량 보존은 격자에 의해 부과된 추가 제한 사항의 적용을 받으며, 이는 주기적 격자 구조를 고려한 양인 quasi-momentum의 보존으로 이어집니다.

​

4. 결정의 분산관계는 에너지-운동량 보존의 nontrivial한 모습입니다

결정의 분산관계는 결정 격자구조의 특정 고려사항과 함께, 에너지(ħω) 및 운동량(ħk) 보존에서 발생한다고 주장할 수 있습니다. 분산 관계는 결정 내에서 전파되는 파동 또는 입자의 에너지와 운동량 사이의 관계를 설명합니다. 주기성 및 전파하는 파동 또는 입자와의 상호 작용과 같은 결정 격자의 고유한 특징은 분산 관계를 형성하는 데 중요한 역할을 합니다.

파동이 결정을 통해 전파되면 격자 전위와 상호 작용하여 보강간섭과 상쇄간섭을 일으킵니다. 이 간섭은 파동의 파장과 격자 간격에 따라 결정을 통과할 때 파동의 모멘텀이 어떻게 변경되는지를 결정합니다. 에너지와 운동량의 보존은 여전히 ​​적용되지만 결정 격자와 특정 특성의 맥락에서 고려되어야 합니다.

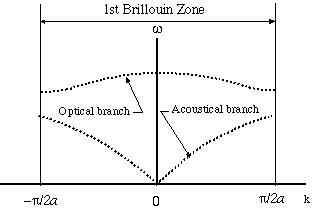
결정에서 분산 관계는 종종 에너지 밴드와 밴드 갭으로 표현됩니다. 이것은 파동의 에너지 준위를 양자화시키는 결정 격자의 주기적 전위로 인해 발생합니다. 결정 격자의 특정 기능과 함께 에너지 및 운동량의 보존은 전파하는 파동에 대한 분산 관계 및 허용된 에너지 상태를 결정합니다.

결론적으로 결정의 분산 관계는 실제로 에너지와 운동량 보존의 직접적인 결과이지만 결정 격자의 특정 특성과 상호 작용도 고려합니다. 결정 격자의 고유한 특성은 결정 내에서 전파되는 파동과 입자의 거동을 결정하는 데 중요한 역할을 하는 분산 관계를 발생시킵니다.

​

5. 입사파 : (에너지 손실 없을경우) 주어진 ħω에 대해 crystal은 허용가능한 k를 알려주고, 결정내부 입자 : 결정 내부의 입자들이 가질 수 있는 ħk를 제한하며 그에따라 ħω도 제한됩니다(discrete하면 energy band 구조)

결정에서 에너지 손실이 없을 때 분산 관계는 실제로 다음과 같이 해석될 수 있습니다. "파동의 주어진 에너지에 대해 결정은 결정 내에서 허용되는 특정 운동량을 허용합니다." 분산 관계는 결정 격자와의 특정 상호 작용을 고려하여 결정 내에서 전파되는 파동 또는 입자에 대한 에너지와 운동량 간의 관계를 설명합니다.

크리스탈 내부에서 보면 "허용된 운동량에 해당하는 에너지 밴드가 존재한다"고 말할 수 있습니다. 에너지 밴드는 결정 내의 파동 또는 입자에 대해 허용된 에너지 상태를 나타냅니다. 이러한 에너지 밴드는 에너지 준위를 양자화하는 결정 격자의 주기적 전위로 인해 발생합니다.

분산 관계는 이러한 허용된 대역 내에서 에너지와 운동량 간의 관계를 제어합니다. 파동의 에너지와 운동량이 보존되기 때문에(결정에서 에너지 손실이 없다고 가정) 분산 관계는 주어진 에너지에 대해 허용된 운동량에 대한 제약으로 작용하거나 그 반대의 경우도 마찬가지입니다.

결론적으로 에너지 손실이 없다는 점을 고려하면 결정의 분산 관계에 대한 해석이 정확합니다. 분산 관계는 결정 격자와의 특정 상호 작용을 고려하여 결정 내에서 전파되는 파동 또는 입자의 주어진 에너지에 대해 허용된 운동량을 설명합니다. 결정의 관점에서 볼 때, 허용 운동량은 결정 격자의 주기적 전위로 인한 에너지 준위의 양자화로 인한 에너지 밴드에 해당합니다.

​

6. 요약 : 방향성이 중요합니다.

외부 -> 결정 : 입사하는 입자(파동)의 에너지 ħω은, 결정 내부에서 허용되는 k값으로 변합니다.

결정 내부 : 결정 내부에서 존재하는 입자들은 양자화되어 허용된 운동량 ħk만을 가질 수 있으며, 이는 또한 에너지의 양자화로 이어집니다.

* 결정 내부의 에너지 공간은 nontrivial한 밀도를 지니지만, 운동량 공간은 trivial하게 경계조건에 의해 정해집니다.

그래서 나중에 나오지만 포논의 비열 기여 등을 계산할 때, 총에너지는 에너지공간 적분이지만, 이 적분의 에너지 밀도를 운동량공간으로 전환시켜서 풀어나갑니다(두 공간을 이어주는 물리량은 입자의 총 갯수 N입니다). 운동량공간의 밀도는 차원과 격자간격에 의해서 constant로 정해지기에.